
नौ नौवीं नहीं, बल्कि 10वीं
हैरी बेकर, लाइव सांइंस के लिए
शोधकर्ताओं ने नौवीं डेडेकाइंड संख्या की गणना की है, जो संख्याओं की एक तेजी से जटिल श्रृंखला से संबंधित है. यह संख्या विभिन्न अंतरिक्ष सम्बन्धी आयामों के आधार पर तार्किक कार्यों के आउटपुट को परिभाषित करती है.
इस आधार पर अब यह कहा जा सकता है कि सुपर कंप्यूटर से लैस गणितज्ञों ने आखिरकार उस बड़ी संख्या के मूल्य की पहचान कर ली है, जिसकी गणना करना पहले असंभव माना जाता था.
वह नंबर, जिसे नौवीं डेडेकाइंड संख्या या डी(9) के रूप में जाना जाता है, वास्तव में अनुक्रम में 10वीं है. प्रत्येक डेडेकाइंड संख्या विभिन्न स्थानिक आयामों में एक निश्चित प्रकार के सच्चे-झूठे तार्किक संचालन की संभावित कॉन्फ़िगरेशन की संख्या का प्रतिनिधित्व करती है. अनुक्रम में पहली संख्या D(0) है, जो शून्य आयामों का प्रतिनिधित्व करती है. यही कारण है कि D(9), जो नौ आयामों का प्रतिनिधित्व करती है, अनुक्रम में 10वीं संख्या है.
प्रत्येक नए आयाम के लिए डेडेकाइंड संख्याएँ उत्तरोत्तर बड़ी होती जाती हैं, जिससे उनका पता लगाना कठिन होता जाता है. आठवीं डेडेकाइंड संख्या, जो आठ आयामों के लिए समान नियमों का पालन करती है, की गणना 1991 में की गई थी, लेकिन नौवीं की गणना के लिए आवश्यक कंप्यूटिंग शक्ति में अप्रत्याशित वृद्धि के कारण, कुछ गणितज्ञों ने इसके सटीक मूल्य की गणना करना असंभव समझा. लेकिन अब, अलग-अलग अनुसंधान समूहों के दो असंबंधित अध्ययनों, जिसका रिसर्च पहला 5 अप्रैल को प्रीप्रिंट सर्वर arXiv को सबमिट किया गया और दूसरा 6 अप्रैल को उसी सर्वर को सबमिट किया गया, ने असंभव को पूरा कर दिया है. इस प्रत्येक अध्ययन के लिए एक सुपर कंप्यूटर का उपयोग किया गया.
हालांकि परिणामों की अभी तक सहकर्मी-समीक्षा नहीं की गई है. फिर भी अध्ययन एक ही निष्कर्ष पर पहुंचे हैं, जिसमें यह "100% निश्चित" है कि संख्या को ठीक से समझा गया है. दूसरे रिसर्च पेपर के मुख्य लेखक, लेनार्ट वान हिर्टम, जर्मनी के पैडरबोर्न विश्वविद्यालय के गणितज्ञ और दूसरे पेपर के प्रमुख लेखक हैं, ने लाइव साइंस को बताया.
वैन हिर्टम और उनके सहयोगियों ने 27 जून को पैडरबोर्न विश्वविद्यालय में एक व्याख्यान के दौरान इसकी जानकारी दी.
डेडेकाइंड नंबर क्या हैं?
डेडेकाइंड संख्याओं का वर्णन सबसे पहले 19वीं शताब्दी में जर्मन गणितज्ञ रिचर्ड डेडेकाइंड द्वारा किया गया था. संख्याएँ तार्किक समस्याओं से संबंधित हैं जिन्हें "मोनोटोन बूलियन फ़ंक्शंस" (एमबीएफ) के रूप में जाना जाता है.
बूलियन फ़ंक्शंस एक प्रकार का तर्क है जो इनपुट के रूप में केवल दो मानों में से एक ले सकता है - 0 (गलत) और 1 (सही) - और केवल उन दो मानों को बाहर निकाल सकता है. एमबीएफ में आप इनपुट में 0 को 1 से स्वैप कर सकते हैं, लेकिन केवल तभी जब यह आउटपुट को 0 से 1 में बदलने की अनुमति देता है, 1 से 0 में नहीं. डेडेकाइंड नंबर एमबीएफ के आउटपुट हैं जहां इनपुट एक है विशिष्ट स्थानिक आयाम.
वैन हर्टम ने इस बारे में समझाया है— यह अवधारणा गैर-गणितज्ञों के लिए काफी भ्रमित करने वाली हो सकती है, लेकिन यह कल्पना करना संभव है कि प्रत्येक आयाम के लिए डेडेकाइंड संख्याओं का प्रतिनिधित्व करने के लिए आकृतियों का उपयोग करके क्या हो रहा है. उदाहरण के लिए, दूसरे आयाम में, डेडेकाइंड संख्या एक वर्ग से संबंधित है, जबकि तीसरे को एक घन द्वारा दर्शाया जा सकता है, और चौथे और उच्चतर को हाइपरक्यूब द्वारा दर्शाया जा सकता है.
प्रत्येक आयाम के लिए, एक विशिष्ट आकार के शीर्ष, या बिंदु, एमबीएफ के संभावित विन्यास का प्रतिनिधित्व करते हैं (नीचे चित्र देखें)। डेडेकाइंड नंबर खोजने के लिए, आप गिन सकते हैं कि आप कितनी बार प्रत्येक आकृति के प्रत्येक शीर्ष को दो रंगों (इस मामले में लाल और सफेद) में से एक के साथ रंग सकते हैं, लेकिन इस शर्त के साथ कि एक रंग (इस मामले में सफेद) नहीं रखा जा सकता है दूसरे के ऊपर (इस मामले में लाल)।
तेजी से जटिल आकृतियों के भीतर रंगीन शीर्षों के संभावित विन्यास को दर्शाने वाला एक आरेख
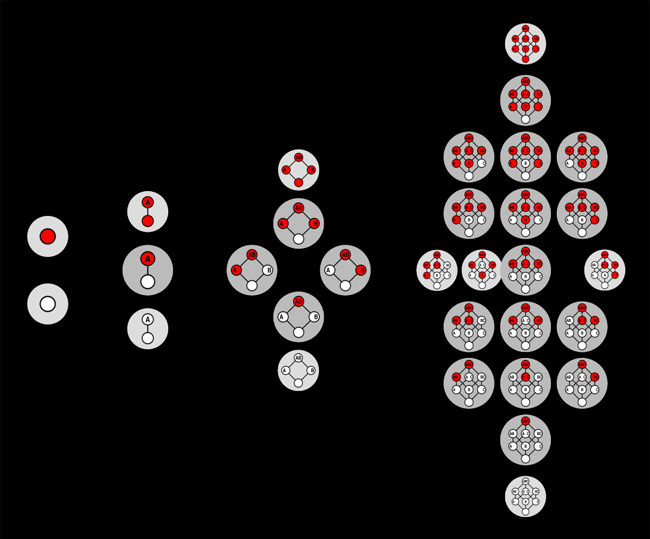
एक आरेख जो पहले चार डेडेकाइंड संख्याओं के लिए आउटपुट दिखाता है: बाएं से दाएं डी(0), डी(1), डी(2), और डी(3)। वृत्त प्रत्येक आकृति के लिए एक संभावित विन्यास का प्रतिनिधित्व करते हैं जहां सफेद शीर्षों को लाल शीर्षों के ऊपर नहीं रखा जाता है। (छवि क्रेडिट: पैडरबोर्न विश्वविद्यालय)
शून्य आयामों के लिए, आकार केवल एक बिंदु है, और D(0)=2 क्योंकि बिंदु या तो लाल या सफेद हो सकता है। एक आयाम के लिए, आकृति दो बिंदुओं वाली एक रेखा है और D(1)=3 क्योंकि दोनों बिंदु या तो एक ही रंग के हो सकते हैं या सफेद के ऊपर लाल हो सकते हैं। दो आयामों के लिए, आकार एक वर्ग है और D(2)=6 है क्योंकि अब छह संभावित परिदृश्य हैं जहां कोई भी सफेद बिंदु लाल बिंदु के ऊपर नहीं है। और तीन आयामों के लिए, आकार एक घन है, और संभावित कॉन्फ़िगरेशन की संख्या बढ़कर 20 हो जाती है, इसलिए D(3)=20।
वान हर्टम ने कहा कि जैसे-जैसे आयामों की संख्या बढ़ती है, काल्पनिक आकार अधिक संख्या में परिणामों के साथ एक जटिल हाइपरक्यूब बन जाता है।
अगले पांच डेडेकाइंड नंबरों के मान 68, 7581, 7828354, 2414682040998 और 56130437228687557907788 हैं।
डी(9) के लिए नया पहचाना गया मान 286386577668298411128469151667598498812366 है।
अधिकाधिक जटिल गणनाएँ
वैन हर्टम तीन साल से अधिक समय से डी(9) की पहचान पर काम कर रहे हैं। ऐसा करने के लिए, उन्होंने एक सुपर कंप्यूटर को एक विशिष्ट तरीके से डेटा को संसाधित करने में सक्षम बनाने के लिए एक नए प्रकार का कंप्यूटर प्रोग्राम बनाया। उन्होंने कहा, यदि उन्होंने अधिक बुनियादी कार्यक्रम का उपयोग किया होता, तो गणनाओं को पूरा करने में 100 साल तक का समय लग सकता था, यहां तक कि एक उन्नत मशीन द्वारा संख्याओं को खंगालने में भी। अपना कंप्यूटर कोड बनाते समय, वैन हर्टम की टीम ने डेटा को संसाधित करने के लिए बेल्जियम के ल्यूवेन विश्वविद्यालय में सुपर कंप्यूटर का उपयोग करते हुए चार महीने से अधिक समय बिताया।
हालाँकि, गणना को पूरा होने में वास्तव में इतना समय नहीं लगा: कार्यक्रम की प्रकृति का मतलब था कि इसमें आंशिक रूप से त्रुटियाँ होने की संभावना थी, जिसका मतलब था कि टीम को लगातार काम फिर से शुरू करना था, वान हर्टम ने कहा।
इसकी तुलना में, 1991 में D(8) पर काम करने के लिए जिस कंप्यूटर का उपयोग किया गया था, वह आधुनिक स्मार्टफोन की तुलना में कम शक्तिशाली था और लगभग 200 घंटों में कार्य पूरा कर लेता था। वान हर्टम ने कहा कि एक आधुनिक लैपटॉप शायद उन गणनाओं को 10 मिनट से भी कम समय में पूरा कर सकता है।
वैन हिर्टम का मानना है कि 10वीं डेडेकाइंड संख्या की गणना के लिए कंप्यूटर प्रसंस्करण शक्ति में समान उछाल की आवश्यकता होगी। "अगर हम इसे अभी कर रहे होते, तो इसके लिए सूर्य की कुल बिजली उत्पादन के बराबर प्रसंस्करण शक्ति की आवश्यकता होती," उन्होंने कहा, जिससे गणना करना "व्यावहारिक रूप से असंभव" हो जाता है।
वान हिर्टम ने कहा कि अधिक जटिल एल्गोरिदम का उपयोग करके प्रसंस्करण शक्ति आवश्यकताओं को कम किया जा सकता है।
उन्होंने आगे कहा, "लेकिन एल्गोरिदम कितना जटिल हो सकता है, इसे लेकर हम एक तरह से असमंजस में हैं।"
हालाँकि, अन्य गणितज्ञ अभी भी आशान्वित हैं कि अंततः D(10) की गणना की जा सकती है, वैन हर्टम ने कहा। साभार: लाइव साइंस